📅 2024年4月13日

📖 青空的b站课程

数据结构

在计算机科学中，数据结构是一种数据组织、管理和存储的格式,它可以帮助我们实现对数据高效的访问和修改。更准确地说,数据结构是数据值的集合，可以体现数据值之间的关系，以及可以对数据进行应用的函数或操作。

⭐️ 为了让我们更加灵活的管理我们的数据，对数据的控制更加灵活，如果我们需要存放数据还需要在这些数据中的某个位置插入一条数据、删除、修改等等，如果只用数据可能就比较乏力

⭐️这里就引出了线性表

线性表是由同一类型的数据元素构成的有序序列的线性结构。线性表中元素的个数就是线性表的长度，表的起始位置称为表头，表的结束位置称为表尾，当一个线性表中没有元素时，称为空表

线性表一般需要包含以下功能：

• 获取指定位置上的元素： 直接获取线性表指定位置 i上的元素。
• 插入元素： 在指定位置 i上插入一个元素。
• 删除元素： 删除指定位置 i上的一个元素。
• 获取长度： 返回线性表的长度

线性表:顺序表示

⭐️ 线性表也是基于数组的，它对数组进行了强化，也就是说存放数据的还是数组的形式，但是可以添加一些其他操作使他强化为线性表，底层依然是顺序存储实现的线性表就叫他顺序表，也就是按照下标一个一个往后走的

代码实例：

1️⃣ 定义一个新的泛型类(因为你在使用的时候你并不能确定数组内部存储什么数据),随后在列表中创建一个 Object类型的数组(泛型类型不能定义为数组)，所有的类型都是继承于 Object，还需要设定一个数组的容量便于后面增加

 public class ArrayList<E> {
     private int  capacity = 10; //数组的大小
     private int size = 0; //已经存放变量的数量
     private Object object = new Object[capacity]; //底层存放的数组
 }

2️⃣ 由于底层还是存放的数组，在加入和删除等等操作都需要遍历遍历整个数组，对整个数组进行操作

1. 插入操作，将插入之前的索引位置后半段的变量都向后移动，在将插入的变量存放下来

        public void addList(E element,int index){
            //首先判断索引的位置错误
            if(index>capacity || index < 0) throw  new IndexOutOfBoundsException("接受的索引位置不正确");
            //遍历索引位置
            for (int i = size; i > index ;i--) object[i] = object[i-1];
            //插入变量
            object[index] = element;
            size++;
        }
    
    //重写toString方法
        @Override
        public String toString() {
            StringBuilder builder = new StringBuilder();
            for (int i = 0; i < size; i++) {
                builder.append(object[i]).append(" ");
            }
            return builder.toString();
        }
   

   在 Main中执行

    public class Main {
        public static void main(String[] args) {
            ArrayList<String> arrayList = new ArrayList<String>();
            arrayList.addList("aaa",0);
            arrayList.addList("bbb",1);
            System.out.println(arrayList.toString());
        }
    }
    
    //输出: aaa bbb 
   

   如果数组达到最大容量了就需要自动增加

      public void addList(E element,int index){
            //首先判断索引的位置错误
            if(index>capacity || index < 0) throw  new IndexOutOfBoundsException("接受的索引位置不正确");
            //判断数组是否达到最大容量
            if (size >= capacity) {
                int newCapacity = capacity + 10;
                Object[] newObject = new Object[newCapacity]; //复制数组不能直接复制需要创建一个新数组接受
                System.arraycopy(object, 0, newObject, 0, size); //直接复制数组的内容
                object = newObject; //更换数组
                capacity = newCapacity; //提高容量
            }
            //遍历索引位置
            for (int i = size; i > index ;i--) object[i] = object[i-1];
            //插入变量
            object[index] = element;
            size++;
        }
   

2. 删除操作，遍历数组将指定索引位置的数覆盖就像

        /*删除操作*/
        public void del(int index){
            //首先判断索引的位置错误
            if(index>capacity || index < 0) throw  new IndexOutOfBoundsException("接受的索引位置不正确");
            //编译数组覆盖掉要删除的索引位置
            for (int i = index; i >0 ; i--) object[i] = object[i--];
            size--;
        }
   

3. 获取指定位置索引的数据

        @SuppressWarnings("unchecked") //屏蔽未经检查警告
        public E search(int index){
            if(index>capacity || index < 0) throw  new IndexOutOfBoundsException("接受的索引位置不正确");
            return (E) object[index]; //数组是Object而返回值是泛型所以说需要强转
        }
   

线性表:链表

** **前面的顺序表是使用数组的方式来进行实现，链表是通过指针完成，链表中有多个节点，它们是可以不连续的分散的，它们内部有一个指针指向下一个节点，然后下一个节点又有一个指针指向它的下一个节点，这样就像一条锁链将它们连接起来，它不需要申请连续的空间，只需要按顺序连接就好了，但是逻辑上每个元素都是相邻的

⭐️ 链表分为带头节点的和不带头节点的，带头节点的表示第一个节点不存放数据，只指向它的后节点

⭐️ 代码实现

1️⃣ 同样的定义一个泛型类

 public class LinkList<E> {
     public final Node<E> haed = new Node<>(null); //表的头节点
     public static class Node<E>{ //链表节点类
         E value; //链表节点存的数据
         Node<E> next; //指向链表的下一个节点
         /*构建方法*/
         public Node(E value) {
             this.value = value;
         }
     }
 }

2️⃣ 同样的链表也需要定义删除和插入操作，但是由于它不是使用链表，所以说并不需要使用遍历整个链表

1. 插入数据，链表的插入可以直接修改需要插入节点的前一个节点的指向地址，使它指向插入节点的地址，然后插入节点的地址指向之前插入索引的节点

        public void add(E element,int index){
            if(index < 0 || index > size) //判读传入的索引是否正确
                throw new IndexOutOfBoundsException("闯入的索引值不正确");
            Node<E> prev = head; //找到对应地址的前驱地址
            for(int i = 0;i < index; i++) prev = prev.next;
            Node<E> node = new Node<>(element); //创建新节点
            node.next = prev.next; //让新的节点指向原本的整个节点
            prev.next = node; //让前驱节点指向新的节点
            size++; //链表数量增加
        }
   

   重写toString方法来打印

   @Override
   public String toString() {
       StringBuilder builder = new StringBuilder();
       Node<E> node = head.next;   //从第一个结点开始，一个一个遍历，遍历一个就拼接到字符串上去
       while (node != null) {
           builder.append(node.element).append(" ");
           node = node.next;
       }
       return builder.toString();
   }
   

2. 删除数据，删除数据就简单直接将前驱节点指向被删除节点的后面节点即可，JVM就会自动回收被删除的节点

public E remove(int index){
    if(index < 0 || index > size - 1)   //同样的，先判断位置是否合法
        throw new IndexOutOfBoundsException("删除位置非法，合法的删除位置为：0 ~ "+(size - 1));
    Node<E> prev = head;
    for (int i = 0; i < index; i++)   //同样需要先找到前驱结点
        prev = prev.next;
    E e = prev.next.element;   //先把待删除结点存放的元素取出来
    prev.next = prev.next.next;  //可以删了
    size--;   //记得size--
    return e;
}

3. 获取索引位置

   public E get(int index){
       if(index < 0 || index > size - 1)
           throw new IndexOutOfBoundsException("非法的位置，合法的位置为：0 ~ "+(size - 1));
       Node<E> node = head;
       while (index-- >= 0)   //这里直接让index减到-1为止
           node = node.next;
       return node.element;
   }
   
   public int size(){
       return size;
   }
   

问题：什么情况下使用顺序表，什么情况下使用链表呢？

• 通过分析顺序表和链表的特性我们不难发现，链表在随机访问元素时，需要通过遍历来完成，而顺序表则利用数组的特性直接访问得到，所以，当我们读取数据多于插入或是删除数据的情况下时，使用顺序表会更好。
• 而顺序表在插入元素时就显得有些鸡肋了，因为需要移动后续元素，整个移动操作会浪费时间，而链表则不需要，只需要修改结点 指向即可完成插入，所以在频繁出现插入或删除的情况下，使用链表会更好。

虽然单链表使用起来也比较方便，不过有一个问题就是，如果我们想要操作某一个结点，比如删除或是插入，那么由于单链表的性质，我们只能先去找到它的前驱结点，才能进行。为了解决这种查找前驱结点非常麻烦的问题，我们可以让结点不仅保存指向后续结点的指针，同时也保存指向前驱结点的指针：

这样我们无论在哪个结点，都能够快速找到对应的前驱结点，就很方便了，这样的链表我们成为双向链表（双链表

————————————————

版权声明：本文为柏码知识库版权所有，禁止一切未经授权的转载、发布、出售等行为，违者将被追究法律责任。

原文链接：https://www.itbaima.cn/document/hnkrjrkm3hjzeq6s

线性表: 栈

⭐️ 栈是一种特殊的线性表，它遵循先入后出，后入先出的概念，你可以把它看作一个筒子，你在筒子里面放盘子 ，一层一层放，如果你想要拿出第一个盘子，就要将它后面的盘子全部拿出；

⭐️ 由于以上特性栈只能在栈顶进行删除和添加操作

栈可以使用顺序表也可以使用链表，使用链表就不需要考虑容量问题

⭐️ 栈的定义，这里使用链表，和链表的定义一样

public class LinkedStack <E>{
    /*使用链表*/
    public final Node<E> head = new Node<>(null); //设置头节点
    int size=0;

    /*链表节点*/
    public static class Node<E>{
        E element;

        Node<E> next;

        public Node(E element) {
            this.element = element;
        }
    }
}

⭐️ 栈的出栈操作

1️⃣ 可以将头节点下一个节点为栈顶，最后的节点为栈尾，需要进行判断这个栈是否为空，如果为空删除会报错，随后直接将头节点的指向直接指向下下个节点

public E pop(){
    if(isEmpty(head)) throw  new NoSuchElementException("栈为空"); //判断栈是否为空
    E e = head.next.element; //提出被删除的元素
    head.next = head.next.next; //直接删除栈顶元素
    size--;
    return e;
}

/*判空操作（判断头节点后面是否为空）*/
public boolean isEmpty(Node<E> head){
    return head.next == null;
}

⭐️ 栈的入栈操作

1️⃣ 同样的入栈也需要在栈顶进行，和链表的插入操作类似，但是这里只需要在栈顶头节点后面操作即可

    public void push(E element){
        Node<E> node = new Node<>(element); //定义新节点
        node.next = head.next; //将新节点的下一个节点指向原来的栈顶节点
        head.next = node; //将头节点下个节点指向新节点
        size++;
    }

2️⃣ 最后重写一下 toString方法

    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        Node<E> topHead = head;
        while (topHead.next != null){ //判断下一个节点的指向是否为空，为空就是最后一个节点
            stringBuilder.append(topHead.next.element).append(" ");
            topHead = topHead.next;
        }
        return stringBuilder.toString();
    }

3️⃣ 测试，可以看到后入栈的节点在栈顶，先入的在栈底，删除也是从栈顶开始删除

public class Main {
    public static void main(String[] args) {
        LinkedStack<String> stack = new LinkedStack<String>();
        //A B C D E依次进栈
        stack.push("A");
        stack.push("B");
        stack.push("C");
        stack.push("D");
        stack.push("E");
        System.out.println(stack.toString());
        System.out.println(stack.pop());
        System.out.println(stack.pop());
        System.out.println(stack.pop());
        System.out.println(stack.pop());
    }
}

//输出:
E D C B A 
E
D
C
B

线性表: 队列

⭐️队列也是一种线性表，它和栈不同的是，它先入先出，后入后出，先入的会从队首先出，后入的加入队尾

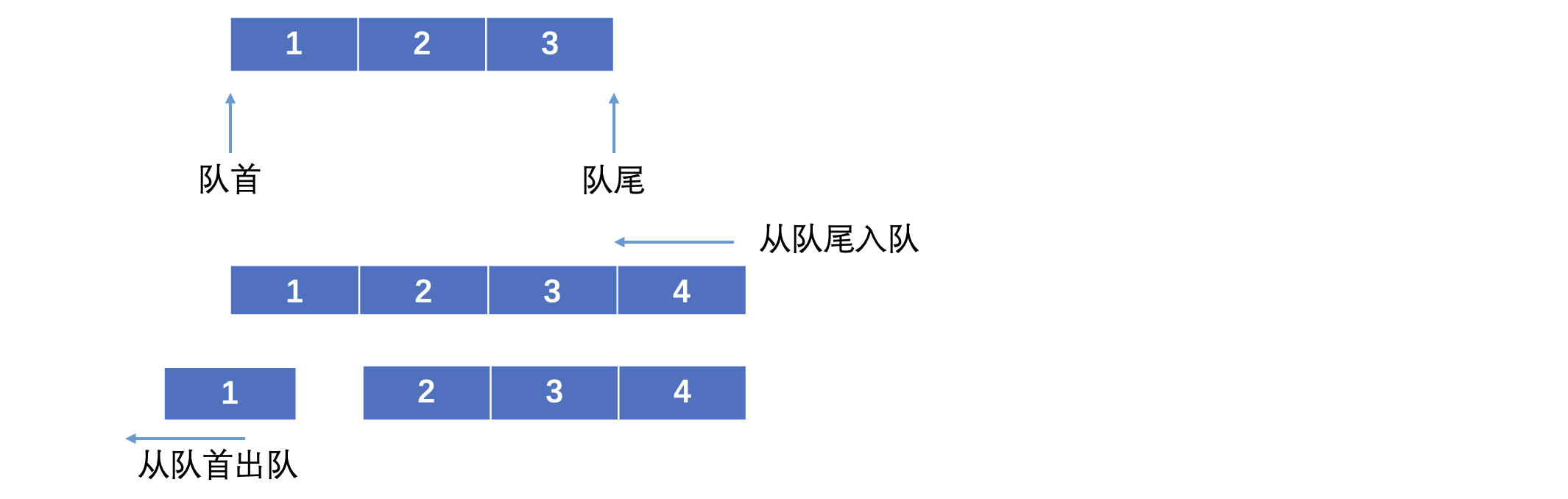
就像超市排队结账，食堂打饭...

⭐️ 队列也可以使用链和顺序表，还是推荐使用链表，更加灵活

public class LinkedQueue <E>{
    public final  Node<E> head = new Node<>(null); //头节点
    int size = 0;
    public static class Node<E>{
        E element;
        Node<E> next;

        public Node(E element){
            this.element = element;
        }
    }
}

⭐️ 队列有入队和出队操作

1️⃣ 入队操作，将入队的节点直接加入队尾，也就是链表的最后一个即可

    /*入队操作*/
    public void enQueue(E element){
        Node<E> tail = head; //定义队尾
        while (tail.next !=null)  tail = tail.next; //获取队尾节点
        tail.next = new Node<E>(element);  //原队尾节点指向新队尾节点
        size++;
    }

2️⃣ 出队操作，直接操作队首，将队首删除

/*出队操作*/
public E deQueue(){
    E e = head.next.element; //提取出队的参数
    head.next = head.next.next; //直接将头节点指向它的下下个节点
    size--;
    return  e;
}

3️⃣ 重写 toString方法

    @Override
    public String toString(){
        Node<E> prev = head;
        StringBuilder stringBuilder = new StringBuilder();
        while (prev.next != null){
            stringBuilder.append(prev.next.element).append(" ");
            prev = prev.next;
        }
        return stringBuilder.toString();
    }

4️⃣ 测试，可以看到先入先出，后入后出

public class Main {
    public static void main(String[] args) {
        LinkedQueue<String> linkedQueue = new LinkedQueue<>();
        linkedQueue.enQueue("A");
        linkedQueue.enQueue("B");
        linkedQueue.enQueue("C");
        linkedQueue.enQueue("D");
        System.out.println(linkedQueue.toString());
        System.out.println(linkedQueue.deQueue());
        System.out.println(linkedQueue.deQueue());
        System.out.println(linkedQueue.deQueue());
        System.out.println(linkedQueue.deQueue());
    }
}

//输出:
A B C D 
A
B
C
D

树:二叉树

⭐️树是一种全新是护具结构，它就像树枝一样，不断的衍生

⭐️可以看到，现在一个结点下面可能会连接多个节点，并不断延伸，就像树枝一样，每个结点都有可能是一个分支点，延伸出多个分支，从位于最上方的结点开始不断向下，而这种数据结构，我们就称为树（Tree）注意分支只能向后单独延伸，之后就分道扬镳了，不能与其他分支上的结点相交！

• 我们一般称位于最上方的结点为树的根结点（Root）因为整棵树正是从这里开始延伸出去的。
• 每个结点连接的子结点数目（分支的数目），我们称为结点的度（Degree），而各个结点度的最大值称为树的度。
• 每个结点延伸下去的下一个结点都可以称为一棵子树（SubTree）比如结点 B及其之后延伸的所有分支合在一起，就是一棵 A的子树。
• 每个结点的层次（Level）按照从上往下的顺序，树的根结点为 1，每向下一层 +1，比如 G的层次就是 3，整棵树中所有结点的最大层次，就是这颗树的深度（Depth），比如上面这棵树的深度为4，因为最大层次就是4。

由于整棵树错综复杂，所以说我们需要先规定一下结点之间的称呼，就像族谱那样：

• 与当前结点直接向下相连的结点，我们称为子结点（Child），比如 B、C、D结点，都是 A的子结点，就像族谱中的父子关系一样，下一代一定是子女，相反的，那么 A就是 B、C、D的父结点（Parent），也可以叫双亲结点。
• 如果某个节点没有任何的子结点（结点度为0时）那么我们称这个结点为叶子结点（因为已经到头了，后面没有分支了，这时就该树枝上长叶子了那样）比如 K、L、F、G、M、I、J结点，都是叶子结点。
• 如果两个结点的父结点是同一个，那么称这两个节点为****兄弟结点（Sibling）比如 B和 C就是兄弟结点，因为都是 A的孩子。
• 从根结点开始一直到某个结点的整条路径的所有结点，都是这个结点的祖先结点（Ancestor）比如 L的祖先结点就是 A、B、E

那么在了解了树的相关称呼之后，相信各位就应该对树有了一定的了解，虽然概念比较多，但是还请各位一定记住，不然后面就容易听懵。

⭐️ 而我们本章需要着重讨论的是二叉树（Binary Tree）它是一种特殊的树，它的度最大只能为 2，所以我们称其为二叉树，一棵二叉树大概长这样：

⭐️并且二叉树任何结点的子树是有左右之分的，不能颠倒顺序，比如A结点左边的子树，称为左子树，右边的子树称为右子树。

当然，对于某些二叉树我们有特别的称呼，比如，在一棵二叉树中，所有分支结点都存在左子树和右子树，且叶子结点都在同一层：

⭐️这样的二叉树我们称为满二叉树，可以看到整棵树都是很饱满的，没有出现任何度为1的结点，当然，还有一种特殊情况：

⭐️ 可以看到只有最后一层有空缺，并且所有的叶子结点是按照从左往右的顺序排列的，这样的二叉树我们一般称其为完全二叉树，所以，一棵满二叉树，一定是一棵完全二叉树。

————————————————

版权声明：本文为柏码知识库版权所有，禁止一切未经授权的转载、发布、出售等行为，违者将被追究法律责任。

原文链接：https://www.itbaima.cn/document/hnkrjrkm3hjzeq6s

⭐️ 二叉树也可以使用链表的形式存储，在节点中存放它的左节点和右节点

1️⃣ 定义一个二叉树

    public static class BinaryTree<E>{
        E element;
        BinaryTree<E> left,right; //指向left和right

        public BinaryTree(E element) {
            this.element = element;
        }
    }

2️⃣ 使用

public class Main {
    public static void main(String[] args) {
        BinaryTree<Character> a = new BinaryTree<Character>('A');
        BinaryTree<Character> b = new BinaryTree<Character>('B');
        BinaryTree<Character> c = new BinaryTree<Character>('C');
        BinaryTree<Character> d = new BinaryTree<Character>('D');
        BinaryTree<Character> e = new BinaryTree<Character>('E');
        //a为root，a的左右节点为b和c，b为a的左节点，它的左右节点为d和e
        a.left = b;
        a.right = c;
        b.left = d;
        b.right= e;
        System.out.println(a.element);
        System.out.println(a.left.element);
        System.out.println(a.right.element);
        System.out.println(a.left.left.element);
        System.out.println(a.left.right.element);
    }
}

//输出:
A
B
C
D
E

⭐️ 二叉树的遍历

二叉树的遍历方法又很多种，分为前序遍历，中序遍历，后序遍历，层次遍历

⭐️ 前序遍历，先遍历每个节点的左节点，在输出右节点

1️⃣ 使用上面定义的二叉树链表

public static void main(String[] args) {
    BinaryTree<Character> a = new BinaryTree<Character>('A');
    BinaryTree<Character> b = new BinaryTree<Character>('B');
    BinaryTree<Character> c = new BinaryTree<Character>('C');
    BinaryTree<Character> d = new BinaryTree<Character>('D');
    BinaryTree<Character> e = new BinaryTree<Character>('E');
    BinaryTree<Character> f = new BinaryTree<Character>('F');
    a.left = b;
    a.right = c;
    b.left = d;
    b.right= e;
    c.right = f;
	preOrder(a);
}

2️⃣ 编写遍历方法，直接使用递归遍历，依照代码执行顺序来执行遍历

    public static void preOrder(BinaryTree<Character> root){
        if(root == null){
            return; //如果节点为空就直接结束
        }
        System.out.println(root.element); //先输入传入节点的参数，如何左右递归遍历
        preOrder(root.left); //遍历每个节点的左部
        preOrder(root.right); //在遍历每个节点的又部
    }

2️⃣调用方法输出

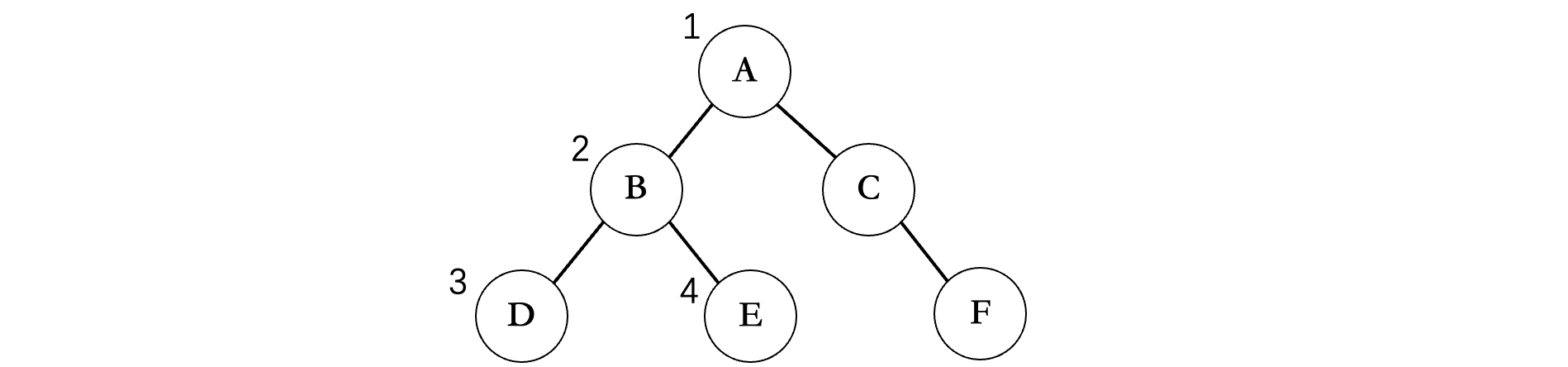
A
B
D
E
C
F

⭐️ 中序遍历，先不断遍历左子树，然后遍历到最底部，但是沿途不打印，到最底部没有左子树了之后在打印，然后在遍历此左子树是否有右子树，没有就返回上层打印上层的数据，然后在遍历上层节点的右子树，如果右就继续遍历，没有就返回

也就是说中序遍历需要将改节点所有左子树全部遍历完成在打印左子树，如果有右子树就在遍历右子树的左子树

1️⃣ 只需要将之前前序方法的代码执行位置修改即可

    /*二叉树的遍历（中序）*/
    public static void inOrder(BinaryTree<Character> root){
        if(root == null){
            return; //如果节点为空就直接结束
        }
        inOrder(root.left); //先遍历每个节点的左子树
        System.out.println(root.element); //如果没有左子树了就输出
        inOrder(root.right); //在遍历每个节点的右子树
    }

2️⃣ 调用执行结果

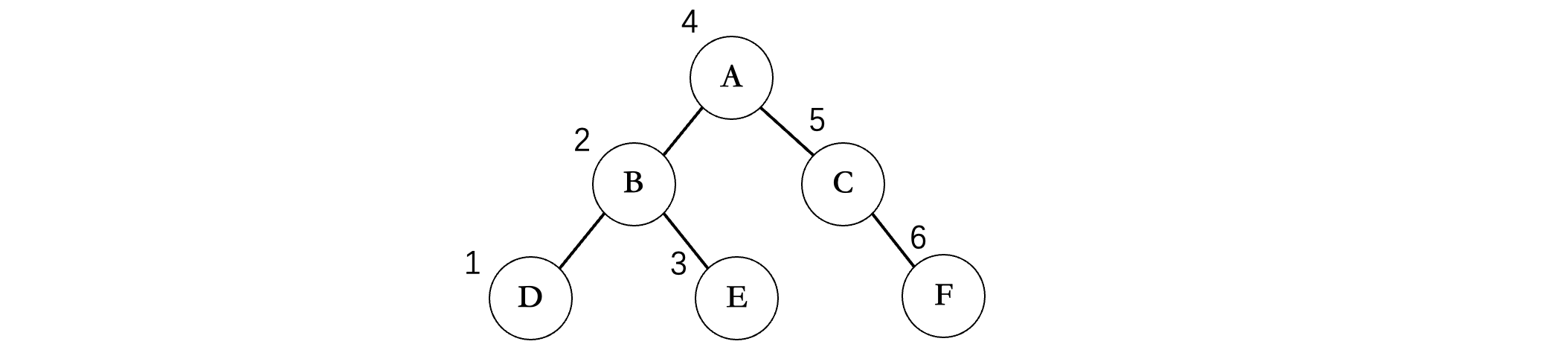
D
B
E
A
C
F

⭐️ 后序遍历，首先还是一路向左，到达最后一个左子树，然后遍历此左子树有没有右子树，如果没有就回到上层，在遍历上层的右子树，

就是将左子树和右子树全部遍历完成在打印此子树

1️⃣ 也只是需要修改即可

    /*二叉树的遍历（后序）*/
    public static void postOrder(BinaryTree<Character> root){
        if(root == null){
            return; //如果节点为空就直接结束
        }
        postOrder(root.left); //先遍历每个节点的左子树
        postOrder(root.right); //在遍历每个节点的右子树
        System.out.println(root.element); //如果没有左子树和右子树了就打印
    }

2️⃣ 输出结果

⚠️ F为4，C为5

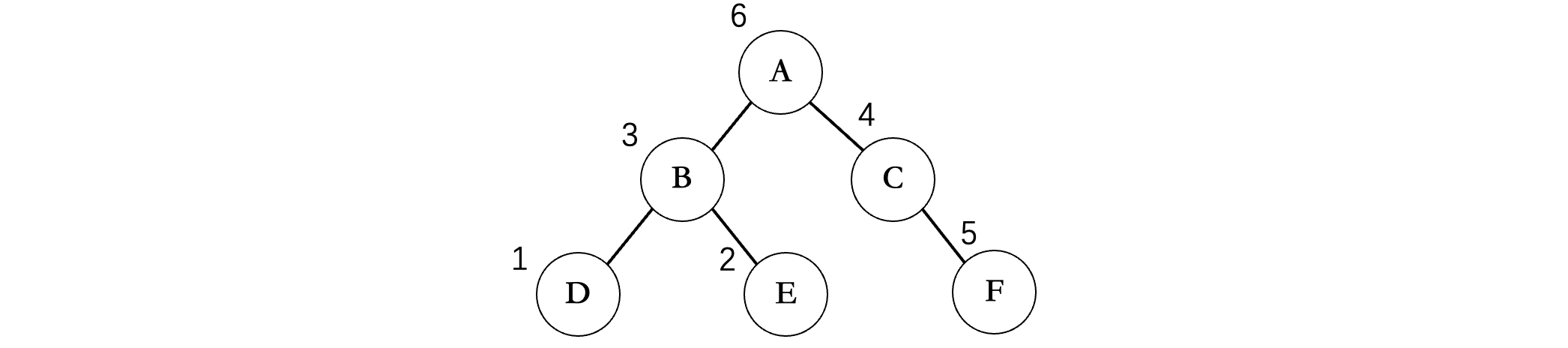
D
E
B
F
C
A

⭐️ 层次遍历

层次遍历是最符合大脑逻辑的一种遍历方式，它是一层一层遍历的，没遍历一层就从左到右打印每个节点

层次遍历可以使用队列来完成，先遍历的树加到队首，后面从左至右的遍历在按照遍历顺序加入队列

1️⃣ 优化一下之前编写的队列代码，加入判空操作；

    /*判空操作*/
    public boolean isEmpty(){
        return head.next == null;
    }

1️⃣ 编写遍历代码

    public static void levelOrder(BinaryTree<Character> root){
        LinkedQueue<BinaryTree> linkedQueue = new LinkedQueue<>(); //创建队列
        linkedQueue.enQueue(root); //将根节点丢入队列中
        while (!linkedQueue.isEmpty()){ //如果队列不为空就一直取出来
            BinaryTree<Character> node = linkedQueue.deQueue(); //去出队首
            System.out.print(node.element);
            if(node.left != null) linkedQueue.enQueue(node.left);   //如果左右孩子不为空，直接将左右孩子丢进队列
            if(node.right != null) linkedQueue.enQueue(node.right);
        }
    }

3️⃣ 输出结果

ABCDEF

树:二叉查找树和平衡二叉树

还记得我们开篇讲到的二分搜索算法吗？通过不断缩小查找范围，最终我们可以以很高的效率找到有序数组中的目标位置。而二叉查找树则利用了类似的思想，我们可以借助其来像二分搜索那样快速查找。

二叉查找树也叫二叉搜索树或是二叉排序树，它具有一定的规则：

• 左子树中所有结点的值，均小于其根结点的值。
• 右子树中所有结点的值，均大于其根结点的值。
• 二叉搜索树的子树也是二叉搜索树。

一棵二叉搜索树长这样：

这棵树的根结点为18，而其根结点左边子树的根结点为10，包括后续结点，都是满足上述要求的。二叉查找树满足左边一定比当前结点小，右边一定比当前结点大的规则，比如我们现在需要在这颗树种查找值为15的结点：

1. 从根结点18开始，因为15小于18，所以从左边开始找。
2. 接着来到10，发现10比15小，所以继续往右边走。
3. 来到15，成功找到。

实际上，我们在对普通二叉树进行搜索时，可能需要挨个进行查看比较，而有了二叉搜索树，查找效率就大大提升了，它就像我们前面的二分搜索那样。

利用二叉查找树，我们在搜索某个值的时候，效率会得到巨大提升。但是虽然看起来比较完美，也是存在缺陷的，比如现在我们依次将下面的值插入到这棵二叉树中：

20 15 13 8 6 3

在插入完成后，我们会发现这棵二叉树竟然长这样：

因为根据我们之前编写的插入规则，小的一律往左边放，现在正好来的就是这样一串递减的数字，最后就组成了这样的一棵只有一边的二叉树，这种情况，与其说它是一棵二叉树，不如说就是一个链表，如果这时我们想要查找某个结点，那么实际上查找的时间并没有得到任何优化，直接就退化成线性查找了。

所以，二叉查找树只有在理想情况下，查找效率才是最高的，而像这种极端情况，就性能而言几乎没有任何的提升。我们理想情况下，这样的效率是最高的：

所以，我们在进行结点插入时，需要尽可能地避免这种一边倒的情况，这里就需要引入****平衡二叉树的概念了。实际上我们发现，在插入时如果不去维护二叉树的平衡，某一边只会无限制地延伸下去，出现极度不平衡的情况，而我们理想中的二叉查找树左右是尽可能保持平衡的，平衡二叉树（AVL树）就是为了解决这样的问题而生的。

它的性质如下：

• 平衡二叉树一定是一棵二叉查找树。
• 任意结点的左右子树也是一棵平衡二叉树。
• 从根节点开始，左右子树都高度差不能超过1，否则视为不平衡。

可以看到，这些性质规定了平衡二叉树需要保持高度平衡，这样我们的查找效率才不会因为数据的插入而出现降低的情况。二叉树上节点的左子树高度 减去 右子树高度， 得到的结果称为该节点的****平衡因子（Balance Factor），比如：

通过计算平衡因子，我们就可以快速得到是否出现失衡的情况。比如下面的这棵二叉树，正在执行插入操作：

可以看到，当插入之后，不再满足平衡二叉树的定义时，就出现了失衡的情况，而对于这种失衡情况，为了继续保持平衡状态，我们就需要进行处理了。我们可能会遇到以下几种情况导致失衡：

根据插入结点的不同偏向情况，分为 LL型、LR型、RR型、RL型。针对于上面这几种情况，我们依次来看一下如何进行调整，使得这棵二叉树能够继续保持平衡：

动画网站：https://www.cs.usfca.edu/~galles/visualization/AVLtree.html（实在不理解可以看看动画是怎么走的）

1. LL型调整（右旋）
   
   首先我们来看这种情况，这是典型的LL型失衡，为了能够保证二叉树的平衡，我们需要将其进行****旋转来维持平衡，去纠正最小不平衡子树即可。那么怎么进行旋转呢？对于LL型失衡，我们只需要进行右旋操作，首先我们先找到最小不平衡子树，注意是最小的那一个：
   
   可以看到根结点的平衡因子是2，是目前最小的出现不平衡的点，所以说从根结点开始向左的三个结点需要进行右旋操作，右旋需要将这三个结点中间的结点作为新的根结点，而其他两个结点现在变成左右子树：
   
   这样，我们就完成了右旋操作，可以看到右旋之后，所有的结点继续保持平衡，并且依然是一棵二叉查找树。
2. RR型调整（左旋）
   前面我们介绍了LL型以及右旋解决方案，相反的，当遇到RR型时，我们只需要进行左旋操作即可：
   
   操作和上面是一样的，只不过现在反过来了而已：
   
   这样，我们就完成了左旋操作，使得这棵二叉树继续保持平衡状态了。
3. RL型调整（先右旋，再左旋）
   剩下两种类型比较麻烦，需要旋转两次才行。我们来看看RL型长啥样：
   
   可以看到现在的形状是一个回旋镖形状的，先右后左的一个状态，也就是RL型，针对于这种情况，我们需要先进行右旋操作，注意这里的右旋操作针对的是后两个结点：
   
   其中右旋和左旋的操作，与之前一样，该怎么分配左右子树就怎么分配，完成两次旋转后，可以看到二叉树重新变回了平衡状态。
4. LR型调整（先左旋，再右旋）
   和上面一样，我们来看看LR型长啥样，其实就是反着的：
   
   形状是先向左再向右，这就是典型的LR型了，我们同样需要对其进行两次旋转：
   
   这里我们先进行的是左旋，然后再进行的右旋，这样二叉树就能继续保持平衡了。

这样，我们只需要在插入结点时注意维护整棵树的平衡因子，保证其处于稳定状态，这样就可以让这棵树一直处于高度平衡的状态，不会再退化了。

树:红黑树

前面我们讲解了二叉平衡树，通过在插入结点时维护树的平衡，这样就不会出现极端情况使得整棵树的查找效率急剧降低了。但是这样是否开销太大了一点，因为一旦平衡因子的绝对值超过1那么就失衡，这样每插入一个结点，就有很大的概率会导致失衡，我们能否不这么严格，但同时也要在一定程度上保证平衡呢？这就要提到红黑树了。

在线动画网站：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

红黑树也是二叉查找树的一种，它大概长这样，可以看到结点有红有黑：

它并不像平衡二叉树那样严格要求高度差不能超过1，而是只需要满足五个规则即可，它的规则如下：

• 规则1：每个结点可以是黑色或是红色。
• 规则2：根结点一定是黑色。
• 规则3：红色结点的父结点和子结点不能为红色，也就是说不能有两个连续的红色。
• 规则4：所有的空结点都是黑色（空结点视为NIL，红黑树中是将空节点视为叶子结点）
• 规则5：每个结点到空节点（NIL）路径上出现的黑色结点的个数都相等。

它相比平衡二叉树，通过不严格平衡和改变颜色，就能在一定程度上减少旋转次数，这样的话对于整体性能是有一定提升的，只不过我们在插入结点时，就有点麻烦了，我们需要同时考虑变色和旋转这两个操作了，但是会比平衡二叉树更简单。

那么什么时候需要变色，什么时候需要旋转呢？我们通过一个简单例子来看看：

首先这棵红黑树只有一个根结点，因为根结点必须是黑色，所以说直接变成黑色。现在我们要插入一个新的结点了，所有新插入的结点，默认情况下都是红色：

所以新来的结点7根据规则就直接放到11的左边就行了，然后注意7的左右两边都是NULL，那么默认都是黑色，这里就不画出来了。同样的，我们往右边也来一个：

现在我们继续插入一个结点：

插入结点4之后，此时违反了红黑树的规则3，因为红色结点的父结点和子结点不能为红色，此时为了保持以红黑树的性质，我们就需要进行****颜色变换才可以，那么怎么进行颜色变换呢？我们只需要直接将父结点和其兄弟结点同时修改为黑色（为啥兄弟结点也需要变成黑色？因为要满足性质5）然后将爷爷结点改成红色即可：

当然这里还需注意一下，因为爷爷结点正常情况会变成红色，相当于新来了个红色的，这时还得继续往上看有没有破坏红黑树的规则才可以，直到没有为止，比如这里就破坏了性质一，爷爷结点现在是根结点（不是根结点就不需要管了），必须是黑色，所以说还要给它改成黑色才算结束：

接着我们继续插入结点：

此时又来了一个插在4左边的结点，同样是连续红色，我们需要进行变色才可以讲解问题，但是我们发现，如果变色的话，那么从11开始到所有 NIL结点经历的黑色结点数量就不对了：

所以说对于这种****父结点为红色，父结点的兄弟结点为黑色（NIL视为黑色）的情况，变色无法解决问题了，那么我们只能考虑旋转了，旋转规则和我们之前讲解的平衡二叉树是一样的，这实际上是一种LL型失衡：

同样的，如果遇到了 LR型失衡，跟前面一样，先左旋在右旋，然后进行变色即可：

而 RR型和 RL型同理，这里就不进行演示了，可以看到，红黑树实际上也是通过颜色规则在进行旋转调整的，当然旋转和变色的操作顺序可以交换。所以，在插入时比较关键的判断点如下：

• 如果整棵树为 NULL，直接作为根结点，变成黑色。
• 如果父结点是黑色，直接插入就完事。
• 如果父结点为红色，且父结点的兄弟结点也是红色，直接变色即可（但是注意得继续往上看有没有破坏之前的结构）
• 如果父结点为红色，但父结点的兄弟结点为黑色，需要先根据情况（LL、RR、LR、RL）进行旋转，然后再变色。

哈希表

在之前，我们已经学习了多种查找数据的方式，比如最简单的，如果数据量不大的情况下，我们可以直接通过顺序查找的方式在集合中搜索我们想要的元素；当数据量较大时，我们可以使用二分搜索来快速找到我们想要的数据，不过需要要求数据按照顺序排列，并且不允许中途对集合进行修改。

在学习完树形结构篇之后，我们可以利用二叉查找树来建立一个便于我们查找的树形结构，甚至可以将其优化为平衡二叉树或是红黑树来进一步提升稳定性。

这些都能够极大地帮助我们查找数据，而散列表，则是我们数据结构系列内容的最后一块重要知识。

散列（Hashing）通过散列函数（哈希函数）将要参与检索的数据与散列值（哈希值）关联起来，生成一种便于搜索的数据结构，我们称其为散列表（哈希表），也就是说，现在我们需要将一堆数据保存起来，这些数据会通过哈希函数进行计算，得到与其对应的哈希值，当我们下次需要查找这些数据时，只需要再次计算哈希值就能快速找到对应的元素了：

散列函数也叫哈希函数，哈希函数可以对一个目标计算出其对应的哈希值，并且，只要是同一个目标，无论计算多少次，得到的哈希值都是一样的结果，不同的目标计算出的结果介乎都不同。哈希函数在现实生活中应用十分广泛，比如很多下载网站都提供下载文件的 MD5码校验，可以用来判别文件是否完整，哈希函数多种多样，目前应用最为广泛的是SHA-1和MD5，比如我们在下载IDEA之后，会看到有一个验证文件 SHA-256校验和的选项，我们可以点进去看看：

点进去之后，得到：

e54a026da11d05d9bb0172f4ef936ba2366f985b5424e7eecf9e9341804d65bf *ideaIU-2022.2.1.dmg

这一串由数字和小写字母随意组合的一个字符串，就是安装包文件通过哈希算法计算得到的结果，那么这个东西有什么用呢？我们的网络可能有时候会出现卡顿的情况，导致我们下载的文件可能会出现不完整的情况，因为哈希函数对同一个文件计算得到的结果是一样的，我们可以在本地使用同样的哈希函数去计算下载文件的哈希值，如果与官方一致，那么就说明是同一个文件，如果不一致，那么说明文件在传输过程中出现了损坏。

可见，哈希函数在这些地方就显得非常实用，在我们的生活中起了很大的作用，它也可以用于布隆过滤器和负载均衡等场景，这里不多做介绍了。

前面我们介绍了散列函数，我们知道可以通过散列函数计算一个目标的哈希值，那么这个哈希值计算出来有什么用呢，对我们的程序设计有什么意义呢？我们可以利用哈希值的特性，设计一张全新的表结构，这种表结构是专为哈希设立的，我们称其为哈希表（散列表）

我们可以将这些元素保存到哈希表中，而保存的位置则与其对应的哈希值有关，哈希值是通过哈希函数计算得到的，我们只需要将对应元素的关键字（一般是整数）提供给哈希函数就可以进行计算了，一般比较简单的哈希函数就是取模操作，哈希表长度是多少（长度最好是一个素数），模就是多少：

比如现在我们需要插入一个新的元素（关键字为17）到哈希表中：

插入的位置为计算出来的哈希值，比如上面是8，那么就在下标位置8插入元素，同样的，我们继续插入27：

这样，我们就可以将多种多样的数据保存到哈希表中了，注意保存的数据是无序的，因为我们也不清楚计算完哈希值最后会放到哪个位置。那么如果现在我们想要从哈希表中查找数据呢？比如我们现在需要查找哈希表中是否有14这个元素：

同样的，直接去看哈希值对应位置上看看有没有这个元素，如果没有，那么就说明哈希表中没有这个元素。可以看到，哈希表在查找时只需要进行一次哈希函数计算就能直接找到对应元素的存储位置，效率极高。

1️⃣ 代码实现

public class HashTable <E>{ //使用泛型
    public int tableSize = 10; //哈希表大小
    public final  Object[] hashTable = new Object[10]; //创建哈希表使用顺序表

    /*插入哈希表*/
    public void insert(E element){
        //得到存放哈希表的索引值
        int index = hash(element);
        hashTable[index] =  element; //存放哈希值
    }

    /*测试是否存在哈希表中*/
    public boolean container(E element){
        int index = hash(element);
        return hashTable[index] == element;
    }

    /*计算hash值*/
    public int hash(E element){
        int hashCode = element.hashCode();
        return hashCode % tableSize; //取模得到存放哈希表的位置
    }
}

2️⃣ 调用测试

    public static void main(String[] args) {
        HashTable<Integer>  hashTable = new HashTable<>();
        System.out.println(hashTable.container(3));
        hashTable.insert(3);
        System.out.println(hashTable.container(3));

    }

⭐️ 但是可能会出现另外一种情况，在取模的时候两个数的值是一样，导致它们会存储在同一个地方，那么现在到底要把谁放进去呢？这样就发生了哈希碰撞也叫哈希冲突

⭐️ 常用的是链接地址法，就是将本来哈希顺序表中的每一个格子变成链表的形式

1️⃣ 代码实现

public class HashTable<E> {
    private final int TABLE_SIZE = 10;
    private final Node<E>[] TABLE = new Node[TABLE_SIZE];

    public HashTable(){
        for (int i = 0; i < TABLE_SIZE; i++)
            TABLE[i] = new Node<>(null);
    }

    public void insert(E element){
        int index = hash(element);
        Node<E> prev = TABLE[index];
        while (prev.next != null)
            prev = prev.next;
        prev.next = new Node<>(element);
    }

    public boolean contains(E element){
        int index = hash(element);
        Node<E> node = TABLE[index].next;
        while (node != null) {
            if(node.element == element)
                return true;
            node = node.next;
        }
        return false;
    }

    private int hash(Object object){
        int hashCode = object.hashCode();
        return hashCode % TABLE_SIZE;
    }

    private static class Node<E> {
        private final E element;
        private Node<E> next;

        private Node(E element){
            this.element = element;
        }
    }
}1

测试

1️⃣ 链表反转206. 反转链表 - 力扣（LeetCode）

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null,node = head;
        while(node != null){
            ListNode tmp = node;
            node = node.next;
            tmp.next = prev;
            prev = tmp;
        }
        return prev;
    }
}

2️⃣ 括号匹配 20. 有效的括号 - 力扣（LeetCode）

import java.util.NoSuchElementException;
class Solution {
    public boolean isValid(String s) {
        LinkedStack<Character> linkedStack =  new LinkedStack<>();
        for (int i = 0; i < s.length(); i++) {
            Character tmp = s.charAt(i);
            if(tmp.equals('(')|tmp.equals('{')|tmp.equals('[')){
                linkedStack.push(tmp);
            }else {
                if(linkedStack.isEmpty()) return false;
                char c = linkedStack.pop();
                if(tmp == ')' && c != '(') return  false;
                if(tmp == '}' && c != '{') return  false;
                if(tmp == ']' && c != '[') return  false;
            }
        }
        return linkedStack.isEmpty();
    }

public static class LinkedStack <E>{
    /*使用链表*/
    public final Node<E> head = new Node<>(null); //设置头节点
    int size=0;

    /*入栈操作*/
    public void push(E element){
        Node<E> node = new Node<>(element);
        node.next = head.next;
        head.next = node;
        size++;
    }

    /*出栈操作*/
    public E pop(){
        if(isEmpty()) throw  new NoSuchElementException("栈为空"); //判断栈是否为空
        E e = head.next.element; //提出被删除的元素
//        Node<E> topHead = head;
//        while(topHead.next != null) topHead = topHead.next;  //找到后面节点为空的节点，后面节点为空就表示到栈底了
        head.next = head.next.next; //直接删除栈顶元素
        size--;
        return e;
    }

    /*判空操作（判断头节点后面是否为空）*/
    public boolean isEmpty(){
        return head.next == null;
    }

    /*链表节点*/
    public static class Node<E>{
        E element;

        Node<E> next;

        public Node(E element) {
            this.element = element;
        }
    }

    /*重写toString方法*/
    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();
        Node<E> topHead = head;
        while (topHead.next != null){
            stringBuilder.append(topHead.next.element).append(" ");
            topHead = topHead.next;
        }
        return stringBuilder.toString();
    }
}
}